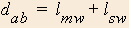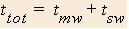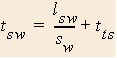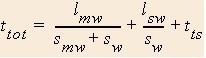Airport Math Puzzle
Page last updated by Steve Greenberg on October 24, 2022 18:47:08 EDT (GMT-0400).
This page has been read 1243 times from 822 internet addresses.
Table Of Contents
Back to Table Of Contents
Questions
The following puzzle was sent to me by Richard H. See if you can figure out the answers before reading my answers.
I was recently at an international airport, trying to get from
one end of a very long terminal to another. It inspired in me the
following simple maths puzzle, which I thought I would share here:
Suppose you are trying to get from one end A of a terminal to the
other end B. (For simplicity, assume the terminal is a
one-dimensional line segment.) Some portions of the terminal have
moving walkways (in both directions); other portions do not. Your
walking speed is a constant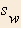 
, but while on a walkway, it is boosted by the speed
of the walkway for a net speed of sw +
smw. (Obviously, given a choice, one would only
take those walkways that are going in the direction one wishes to
travel in.) Your objective is to get from A to B in the shortest
time possible.
- Suppose you need to pause for some period of time, say to tie your shoe. Is it more efficient to do so while on a walkway, or off the walkway? Assume the period of time required is the same in both cases.
- Suppose you have a limited amount of energy available to
run and increase your speed to a higher quantity
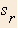(or sr +
smw, if you are on a walkway). Is it more
efficient to run while on a walkway, or off the walkway? Assume
that the energy expenditure is the same in both cases. - Do the answers to the above questions change if one takes into account the various effects of special relativity? (This is of course an academic question rather than a practical one. But presumably it should be the time in the airport frame that one wants to minimise, not time in one's personal frame.)
It is not too difficult to answer these questions on both a rigorous mathematical level and a physically intuitive level, but ideally one should be able to come up with a satisfying mathematical explanation that also corresponds well with one's intuition.
Back to Table Of Contents
Answers
Let us first define some variables.
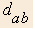
- Distance from a to b
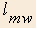
- Length of moving walkway
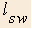
- Length of stationary walkway
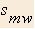
- Speed of moving walkway
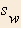
- Walking speed
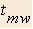
- Time on moving walkway
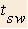
- Time on stationary walkway
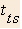
- Time tying shoe
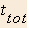
- Total time
Now define some relationships.
Back to Table Of Contents
Answer To Question 1
First consider the case where you tie your shoe while stationary.
Now consider the case where you tie your shoe while on the moving walkway.
- Length on moving walkway while tying your shoe
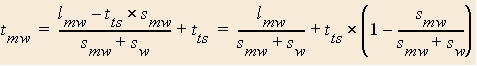
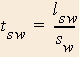
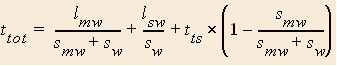
All the numbers in parentheses in the above equation are positive numbers. Therefore the whole parenthesized expression is a number less than 1. Clearly the time to get from a to b is less if you tie your shoe while on the moving walkway. In this case you are at least making some progress while tying your shoe.
Back to Table Of Contents
Answer To Question 2
Just to reduce the number of cases we need to consider, let us assume that the time spent running is less than or equal to the time spent on the moving walkway or the time spent on the stationary walkway, whichever is less.
Define some more variables:
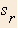
- Running speed
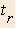
- Time spent running
First consider the case where you are running while on the stationary walkway.
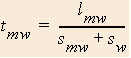
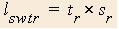
- Length while running on the stationary walkway
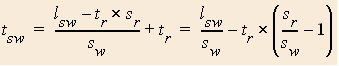
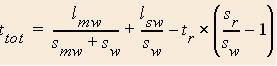
Now consider the case where you are running while on the moving walkway.
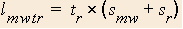
- Length while running on the moving walkway
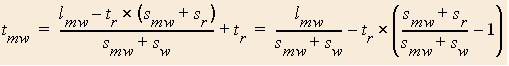
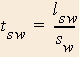
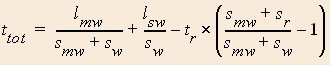
The only difference in the equations for the total times is between the quantities in the parentheses of each equation.
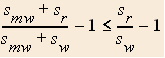
We can see that the above relation is true by testing it at several corner cases.
When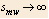 
we have:
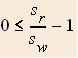
By definition the running speed is greater than the walking speed.
When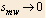 
the two sides are equal.
So for any val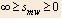ue 
the
relation is true.
This means that the total time for running on the moving walkway is having a smaller quantity subtracted than is the total time for running on the stationary walkway, the total time for running on the stationary walkway is smaller than the total time for running on the moving walkway.
Clearly the time to get from a to b is less if you run while on the stationary walkway than if you run on the moving walkway.
The answers to the two questions seem to be consistent. If you are going to do something to slow down your unassisted pace, better to do it on the moving walkway. If you are going to do something to speed up your unassisted pace, better to do it on the stationary walkway. You minimize the loss by doing it on the moving walkway. You maximize the gain by doing it on the stationary walkway.
Back to Table Of Contents
Answer To Question 3
Since special relativity will just affect the lengths in the above equations, it will not change the answers as to which total times are shorter or longer. (This is my first order intuition.)